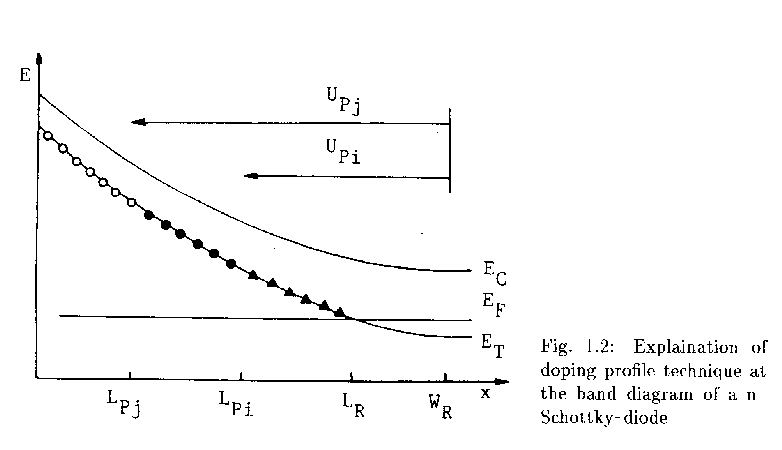
- Measurement at constant reverse bias, variation of pulse voltage,
building difference of transients
At the U-DLTS-method you get from the integration of the Poisson equation
for the voltage transient Ui(t) with the pulse voltage UPi:
|
| |
|
|
|
- |
q
e
|
|
LR
ó
õ
LPi
|
xNT(x) exp(-t/te) dx |
| (1.38) | |
|
|
q
e
|
|
æ
ç
è
|
|
NSWR2
2
|
- |
WR
ó
õ
LR
|
xNT(x) dx |
ö
÷
ø
|
-UD |
| (1.39) |
| |
|
For the difference of two transients with pulse voltages UPj and UPi
are only the traps between LPj and LPi relevant for the signal:
|
Uji(t) : = Uj(t)-Ui(t) = - |
q
e
|
|
LPi
ó
õ
LPj
|
xNT(x)exp(-t/te) dx |
| (1.40) |
With the definition of a medium trap concentration you get the following
approximation:
|
| |
|
|
|
- |
q
2e
|
(LPi2-LPj2) |
_
N
|
T
|
(xji) exp(-t/te) |
| (1.41) | |
|
| (1.42) |
| |
|
The amplitude of charge is then:
|
DUji = - |
q
2e
|
(LPi2-LPj2) |
_
N
|
T
|
(xji) |
| (1.43) |
You can calulate the medium trap concantration following:
|
|
_
N
|
T
|
(xji) = - |
2e
q
|
|
DUji
(LPi2-LPj2)
|
|
| (1.44) |
For the C-DLTS-method you get approximately:
|
|
_
N
|
T
|
(xji) = |
2NSe2F2
CR3
|
|
DCji
(LPi2-LPj2)
|
|
| (1.45) |
DCji is the amplitude difference of the two capacitance transients.
For this technique you must make a measurement in 4.7.2.1 and a evaluation
in 4.1.4.3. In menu 4.7.4.1 you get a NT(x)-plot without building of
differences. This yields normally to a big error because you have in this
case a very brought xRi-range.
- Measurement at constant pulse voltage, variation of revese bias,
building difference of transients
This technique is analog to technique (a). The disadvantage of this method
is that the relevant charges are at the intersection Fermi/trap level.
You can make this measurement in 4.7.2.2.
- Measurement at variation of reverse bias and pulse voltage
A profile analysis is also possible without building of differences:
|
| |
|
|
|
2 NS |
DCi
CRi
|
|
WRi2
LRi2-LPi2
|
for C-DLTS |
| (1.46) | |
|
| DU |
2CRi2
qeF2
|
|
WRi2
LRi2-LPi2
|
for U-DLTS |
| (1.47) |
| |
|
For this technique you must make a measurement in 4.7.2.3 and a evaluation
in 4.1.4.1.
1.3 Kinetic
For the with electrons filled traps nTe is valid during the emission
process:
|
| |
|
|
| (1.48) | |
|
|
æ
ç
è
|
sn vth,n Xn NC exp |
æ
ç
è
|
- |
EC-ET
kT
|
ö
÷
ø
|
ö
÷
ø
|
-1
|
|
| (1.49) |
| |
|
NT is the trap concentration, Xn the entropy factor, sn
the capture cross section for electrons and te the emission time
constant. In the software te is called time constant, emission time
constant, tau or tau_e.
The emission rate is the reziproke value of the emission time
constant:
You get the thermal velocity vth,n and the state density NC from:
|
| |
|
|
| (1.51) | |
|
| 2 |
æ
ç
è
|
2 pm*n kT
h2
|
ö
÷
ø
|
3/2
|
|
| (1.52) |
| |
|
m*n is the effective mass for electrons.
Transforming of eqn. (1.49) yields to the Arrhenius-equation:
|
ln(te vth,n NC) = |
EC-ET
k
|
|
1
T
|
-ln(Xn sn) |
| (1.53) |
By the linear regression you get from the slope EC-ET and from the
intersection the product sn Xn. This equation contains the
T2-correction.
In the program sn Xn will called as capture cross section, sigma or
sig. In the library part of the software the name is Sigma Arrhenius,
Sigma-Arrh or sig-Arrh.
One of the text possiblity for the y-axis of the Arrhenius plot is ln(tau*T2*C).
C means here all constants of vth,n NC except of the temperature.
So C is [(vth,n NC)/( T2)] for electrons and [(vth,p NV)/( T2)]
for holes. tau of the y-axis-text is the emission time constant te.
For the with electrons filled traps nTc is valid during the capture
process:
|
| |
|
|
|
NT |
æ
ç
è
|
1-exp |
æ
ç
è
|
- |
t
tc
|
ö
÷
ø
|
ö
÷
ø
|
|
| (1.54) | |
|
| (1.55) |
| |
|
tc is the capture time constant. In the software tc is called
capture time constant or tau_c. Following is valid:
|
| |
|
|
|
sn vth,n n0 = 1/tc capture rate |
| (1.56) | |
|
|
sn vth,n capture coefficient |
| (1.57) | |
|
| NC exp |
æ
ç
è
|
- |
EC-EF
kT
|
ö
÷
ø
|
|
| (1.58) |
| |
|
The program takes NS as n0.
In the program sn will called as capture_c cross section, sigma_c
or sigmaC. In the library part of the software the name is Sigma Capture
or sig-Capt.